Dynamic Bernstein–Vazirani¶
Here we will demonstrate correcting mid-circuit measurements using the dynamic version of the Bernstein-Vazirani algorithm.
Frontmatter¶
[1]:
import numpy as np
from qiskit import *
from qiskit_ibm_runtime.fake_provider import FakeKolkata, FakeKolkataV2
import mthree
import matplotlib.pyplot as plt
plt.style.use('quantum-light')
Set target noisy simulator
[2]:
backend = FakeKolkata()
Circuit generation function¶
[3]:
def dynamic_bv(bitstring):
"""Create a Bernstein-Vazirani circuit from a given bitstring.
Parameters:
bitstring (str): A bitstring.
Returns:
QuantumCircuit: Output circuit.
"""
qc = QuantumCircuit(2, len(bitstring))
# Prepare the |-x> state on target qubit
qc.x(1)
qc.h(1)
# For each bit (0 or 1) build a simple circuit block
for idx, bit in enumerate(bitstring[::-1]):
# Initial H gate on control
qc.h(0)
# If bit=1, do a CNOT gate
if int(bit):
qc.cx(0, 1)
# Final H gate to convert phase to computational-basis
qc.h(0)
# Measure
qc.measure(0, idx)
# If not at the final bit, recycle and reset qubits
if idx != (len(bitstring)-1):
# Reset control qubit for reuse
qc.reset(0)
# reset target qubit to minimize dephasing
qc.reset(1)
# Prepare the |-x> state on target qubit again
qc.x(1)
qc.h(1)
return qc
Problem setup¶
First we select a range of bit-string lengths to generate. We then use this range to make all-ones bit-string circuits of those lengths.
[4]:
bit_range = range(2, 31)
circs = [dynamic_bv('1'*N) for N in bit_range]
Next, we transpile the circuits for our target backend (simulator in this case):
[5]:
trans_circs = transpile(circs, backend, optimization_level=3)
Next, we determine which qubits are measured to which classical bits using the final_measurement_mapping utility:
[6]:
mappings = mthree.utils.final_measurement_mapping(trans_circs)
# Show a few of the mappings
mappings[:3]
[6]:
[{0: 25, 1: 25}, {0: 25, 1: 25, 2: 25}, {0: 25, 1: 25, 2: 25, 3: 25}]
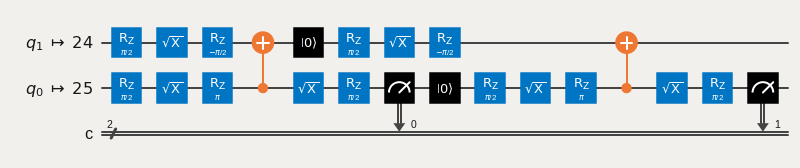
Lets draw the 0th circuit to verify that the mapping is indeed correct:
[7]:
trans_circs[0].draw('mpl', idle_wires=False)
[7]:
Run experiment and mitigate¶
Here we execute the dynamic BV ciruits at 10,000 shots each.
[8]:
shots = int(1e4)
counts = backend.run(trans_circs, shots=shots).result().get_counts()
Next we follow the usual M3 receipe to mitigate the counts. Note that the mappings have all the necessary information for correcting mid-circuit measurements.
[9]:
mit = mthree.M3Mitigation(backend)
[10]:
mit.cals_from_system(mappings)
[11]:
quasis = mit.apply_correction(counts, mappings)
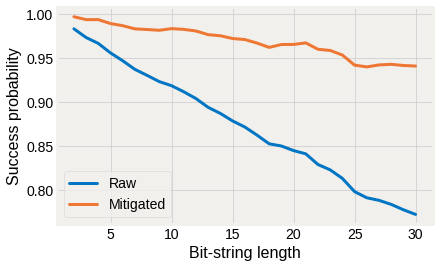
Because we generated all-ones bit-strings, our success criteria is the probability of being found in that state. We can extract this probabilty from both the raw counts and the mitigated quasi-distributions
[12]:
count_probs = [counts[idx].get('1'*num_bits)/shots \
for idx, num_bits in enumerate(bit_range)]
quasi_probs = [quasis[idx].get('1'*num_bits) \
for idx, num_bits in enumerate(bit_range)]
Plot the results¶
[13]:
fig, ax = plt.subplots()
ax.plot(bit_range, count_probs, label='Raw')
ax.plot(bit_range, quasi_probs, label='Mitigated')
ax.set_ylabel('Success probability')
ax.set_xlabel('Bit-string length')
ax.legend();
[ ]: